Урок 5. Функция - Материалы к изучению

Здравствуйте, ученики! 

На сегодняшнем уроке: 

• узнаем понятие функции и график функции; 
• изучим способы задания функции.

• зная определение функции y=kx, построим график и определим ее расположение относительно коэффициента k;  
• узнаем определение линейной функции вида y = kx + b, нарисуем ее график и определим положение графика по отношению к коэффициентам k и b

Термин «функция» происходит от латинского слова functio, что в переводе означает «исполнение», «совершение».  

Термин был впервые введен в 1694 году немецким математиком и ученым Готфридом Вильгельмом Лейбницем (1646-1716).

Определение. Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.

Элемент 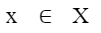называют аргументом функции или независимой переменной.

Элемент 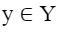называют значением функции или зависимой переменной.

Написание:  y = f(x).  

Пример 1. Автомобиль двигается по трассе с постоянной скоростью 80 км/ч. Необходимо найти путь S км, по которому он проходит за время t. 

Решение:

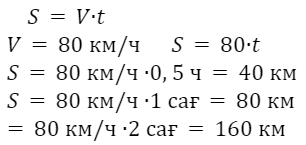
Мы увидели, что если одна переменная изменяет независимую переменную t, то другая переменная меняет зависимую переменную S.

Понятно, что каждому значению независимой переменной соответствует только одно значение зависимой переменной.

Пример 2.

Администрация намерена выделить жителям земельные участки прямоугольной формы площадью 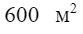каждый. Если один размер земельного участка равен х метрам, то как определить его второй размер y?

рассмотрим х и у как переменные. 

Каждому значению x соответствует только одно значение y. 

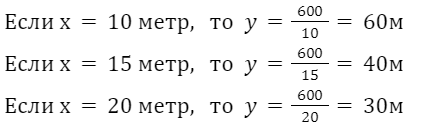
Для определения функции:

1) Должна быть дана закономерность f, устанавливающая функциональную зависимость. Также дается формулой (выражением).  

Например:  

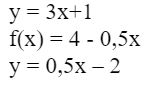
2) Должно быть указано множество возможных значений аргумента. Это множество называется областью определения функции.

Областью значений функции y=f(x) называется множество всех действительных значений

Например: 

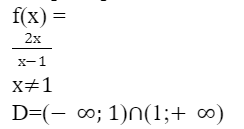
Способы задания функции

1. Аналитический способ: например у=2х+1
2. Табличный способ

1. Графический способ

4. Словесный способ: зависимая переменная на 1 больше удвоенного значения независимой переменной.

Функция прямой пропорциональности

Формула:     y=k∙x

здесь   

k - заданное постоянное число, которое 

называется коэффициентом пропорциональности.

Область определения:

 -∞;+∞.

Свойства прямой пропорциональной функции

1. различные соответствующие значения переменных х и у взаимно пропорциональны, то есть 

Поэтому k-называется коэффициентом пропорциональности. 

Также называют угловым коэффициентом данной прямой: Так как число k зависит от угла между графиком у=kx и осью Ох. 

1. график функции у=kx-прямая линия, проходящая через начальную точку координат О(0;0).  

Пример 1.

Построите график функции у=2х.  

Решение: Составляем таблицу. у=2х   

y=2∙-4=-8 

y=2∙-3=-6

y=2∙-2=-4

y=2∙-1=-2

y=2∙0=0

y=2∙1=2

y=2∙2=4

y=2∙3=6

y=2∙4=8

в результате изобразим полученные точки на координатной плоскости или кратко построим график функции у = 2х.  

Решение: Составляем таблицу. у=2х.

Для построения прямой достаточно двух точек.

в результате изобразим полученные точки на координатной плоскости.

Пример 2.

Построите график функции y=-12∙x  

Решение: Составляем таблицу. 

y=-12∙x 

y=-12-4=2

y=-12-3=-1,5

y=-12-2=1

y=-12-1=0,5

y=-12∙0=0

y=-12∙1=-0,5

y=-12∙2=-1

y=-12∙3=-1,5

y=-12∙4=-2

Или возьмем только две точки и построим график:

Линейная функция и ее график

у=kx+b

называется линейной функцией. 

k и  b – заданные числа. 

k – угловой коэффициент, 

а b свободный член

если х=0,   то у=b. 

прямая, график которой пересекает ось ОУ в точке (0; b). 

Линейная функция и её график

у=kx+b
 

Пример 1.

Построите график функции y=0,5∙x-1  

Решение: Составить таблицу значений функции.  

Пример 2.

Построите график функции y=3-23∙x   

Решение: 

график функции проходит через точку (0; 3). 

Достаточно, если мы определим еще одну точку. 

 x=3  тогда  y=3-23∙3=1 то есть 3;1 проходит через точку. 

Пример 3.

Нужно составить уравнение прямой, показанное на рисунке.

Решение:

А(0;2)  B(4;0)   у=kx+b

2=k∙0+b

и

 0=k∙4+b

то есть b=2; k=-12

y=-12∙x+2 

Проверка: возьмем точку С(2;1) по прямой:

y=-12∙2+2=1 

Ответ:

y=-12∙x+2