Урок 3. Одночлен - Материалы к изучению

Здравствуйте, ученики!

На сегодняшнем занятии:

• узнаете определение одночлена, 
• научитесь определять коэффициент и степень одночлена, а также приводить его в стандартный вид 

Выражение, представляющее собой произведение чисел, переменных и их степеней, называется одночленом. 

Например:

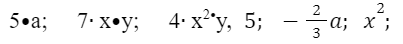
Стандартный вид одночлена 

Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных.

Например:

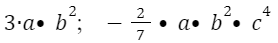
(здесь числовой множитель  3-коэффициент одночлена, остальные множители - переменные и их степени)

(числовой множитель - коэффициент одночлена и переменные и их степени)

Как приводить одночлен к стандартному виду

Чтобы привести одночлен к стандартному виду, его необходимо упростить, воспользовавшись переместительным и сочетательным свойствами умножения. 

Например: 

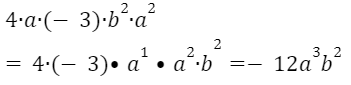
Например:

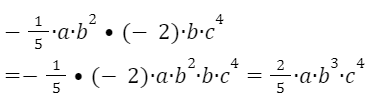
В стандартном виде одночлена переменные следует располагать в алфавитном порядке.

Степень одночлена

Степенью одночлена называют сумму показателей степеней всех входящих в него переменных

Примеры: 

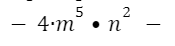степень одночлена равна 7. 

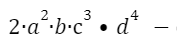степень одночлена равна 10. 

5 - степень одночлена равна 0, так как одночлен не содержит переменных. 

Как умножать одночлены:

1. отдельно умножить их коэффициенты;
2. сложить показатели степеней одинаковых переменных;  
3. переменные, входящие в состав только одного из множителей, перенести в произведение без каких-либо изменений; 
4. затем полученные произведения нужно сложить между собой. 

Например:

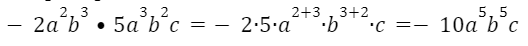
Возведение одночлена в степень:

1. возвести каждый множитель в данную степень по отдельности; 
2. перемножить полученные результаты.

Например:

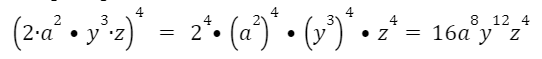
Рассмотрим следующие задания:

1. Определите коэффициент одночлена: 

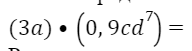
Решение: 

Приводим одночлен к стандартному виду, используя переместительные и сочетательные свойства умножения:

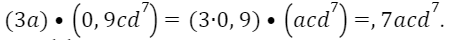
Ответ: коэффициент одночлена  2,7

1. Определите степень одночлена: 

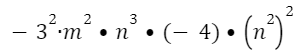
Решение: 

1)  приводим одночлен в стандартный вид:

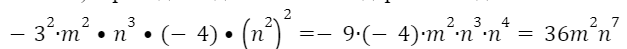
2) Определяем степень одночлена:

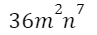
Ответ: степень одночлена равна 9. 

1. Отношение сторон прямоугольника равно 5 :4. Найди длину ребер, если площадь прямоугольника равна 500 дм2. 

Решение: 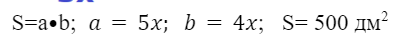  составляем уравнение: