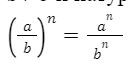Урок 1. Степень с натуральным показателем и ее свойства - Материалы к изучению

Здравствуйте, ученики! Чему Вы научитесь:

Вы узнаете определение степени с натуральным показателем и ее свойства 

Алгебра – раздел математики. Среднеазиатский математик и астроном Мухаммед аль-Хорезми в своей работе «Китаб аль-джебр валь-мукабала» приводит общие правила решения уравнений первой степени. Именно от названия этой книги аль-Джебр (восстановление) и произошло слово «алгебра». 

СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ 

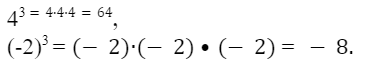
СВОЙСТВА:

1. УМНОЖЕНИЕ СТЕПЕНЕЙ    

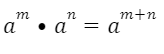
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.

Например: 

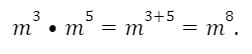
2. ДЕЛЕНИЕ СТЕПЕНЕЙ

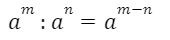
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным 

3.   Любое число в нулевой степени, за исключением нуля, равно единице.

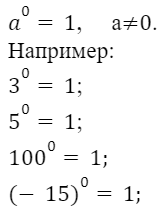
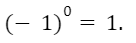
4. ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПРОИЗВЕДЕНИЯ 

Для любых чисел а и b и любого натурального числа n справедливо равенство:    

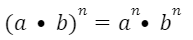
При возведении произведения в степень каждый

множитель возводят в степень и полученные

результаты перемножают.    

Например:

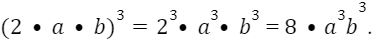
5. Четная степень отрицательного числа есть число положительное. Нечетная степень отрицательного числа есть число отрицательное. 

6. ВОЗВЕДЕНИЕ ДРОБИ В СТЕПЕНЬ 

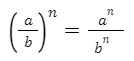
для любых чисел а и b (b≠0) и любого натурального числа n

При возведении дроби в степень нужно возводить отдельно числитель и знаменатель дроби в эту степень.   

Например:      

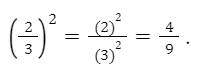
7. ВОЗВЕДЕНИЕ СТЕПЕНИ В СТЕПЕНЬ 

Для любого числа а и любых натуральных чисел m и n справедливо равенство: 

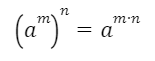
При возведении степени в степень показатели перемножаются, а основание остается прежним.

Например:    

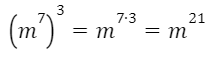
Для любых чисел а и b

b≠0 и натурального числа n, выполняется данное равенство