Урок 6. Квадратичная функция y=ax2 и ее график - Материалы к изучению
Здравствуйте, ученики!
На сегодняшнем занятии:
узнаете как строить график функции
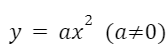
и описывать ее свойства.
Для построения графика функции
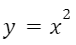
заполняем таблицу.
|
Х |
У |
|
-2 |
4 |
|
-1,5 |
2,25 |
|
-1 |
1 |
|
-0,5 |
0,25 |
|
0 |
0 |
|
0,5 |
0,25 |
|
1 |
1 |
|
1,5 |
2,25 |
|
2 |
4 |
На координатной плоскости отмечаем заданные точки и последовательно соединяем их.
Свойства:
- график функции
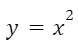называется параболой; - график функции 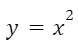главная точка координат проходит через точку О (0;0);
- график функции 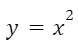располагается выше оси Ох.
- выполняется равенство
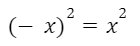график функции 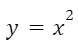симметричен относительно оси ординат.
Название Парабола впервые было введено в работе «Конические сечения» древнегреческим ученым Аполлоном, который жил в III веке до нашей эры.
Свойства параболы широко используются в науке и технике.
Давайте рассмотрим случай, когда a>1:
Например: a=2;
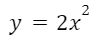
Сравним его с функцией
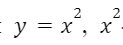
-увеличили в два раза, то значение функции увеличивается в 2 раза:
Например: a=2;
|
х |
y=x2 |
y=2x2 |
|
-2 |
4 |
8 |
|
-1,5 |
2,25 |
4,5 |
|
-1 |
1 |
2 |
|
-0,5 |
0,25 |
0,5 |
|
0 |
0 |
0 |
|
0,5 |
0,25 |
0,5 |
|
1 |
1 |
2 |
|
1,5 |
2,25 |
4,5 |
|
2 |
4 |
8 |
Рассмотрим случай, когда 0<a < 1
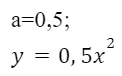
Сравним его с функцией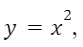 
, делим значение 
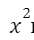на 2, и значение функции уменьшается в 2 раза:
|
х |
y=x2 |
y=0,5x2 |
|
-2 |
4 |
2 |
|
-1,5 |
2,25 |
1,125 |
|
-1 |
1 |
0,5 |
|
-0,5 |
0,25 |
0,125 |
|
0 |
0 |
0 |
|
0,5 |
0,25 |
0,125 |
|
1 |
1 |
0,5 |
|
1,5 |
2,25 |
1,125 |
|
2 |
4 |
2 |
График:
:
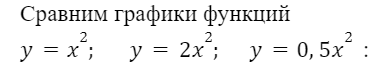