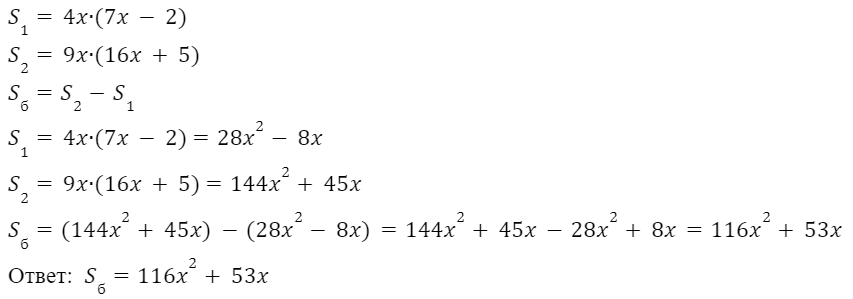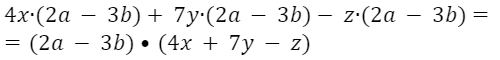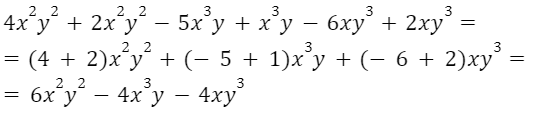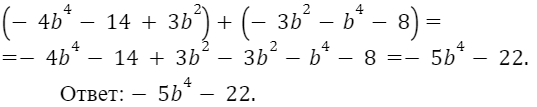Урок 4. Многочлен - Материалы к изучению

Здравствуйте, ученики! На сегодняшнем занятии:

познакомитесь с определением многочлена; 

научитесь находить степень многочлена; 

научитесь приводить многочлен к стандартному виду;

научитесь складывать и вычитать многочлены;

научитесь умножать многочлен на одночлен и многочлен.

Многочлен

Многочленом называется алгебраическая сумма нескольких одночленов. Одночлены, из которых составлен многочлен, называют членами многочлена. 

Например:

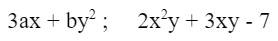
Если многочлен состоит из двух членов, его называют двучленом, если из трех членов — трехчленом.

Подобные члены  

Одночлены называются подобными, если они отличаются коэффициентами или ничем не отличаются друг от друга . Например,

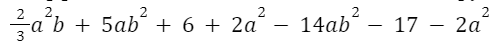
подобные члены многочлена:  

Например:

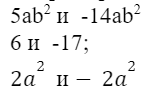
противоположные члены

Приведение подобных членов 

Замена алгебраической суммы подобных членов одним членом, тождественным этой сумме, называется приведением подобных членов.

Таким образом, приведение подобных членов есть тождественное преобразование.

Степень многочлена

Степенью многочлена называют наивысшую степень входящих в него одночленов. 

Например:

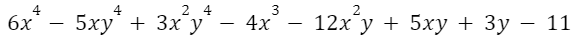
Степень многочлена равна 6, поскольку наивысшая степень 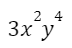одночлена 2+4=6. 

Многочлен стандартного вида

Многочлен стандартного вида – это многочлен, в котором каждый член многочлена является одночленом стандартного вида, нет подобных членов и одночлены расположены в порядке убывания. Например:

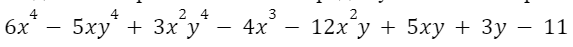
Сложение и вычитание многочленов 

При сложении и вычитании многочленов важно уметь использовать правила раскрытия скобок:

• Если перед скобками стоит знак «+» (плюс), то все числа, стоящие внутри скобок, сохраняют свой знак.
• Если перед скобками стоит знак «–» (минус), то все числа, стоящие внутри скобок, меняют свой знак на противоположный.

Например:

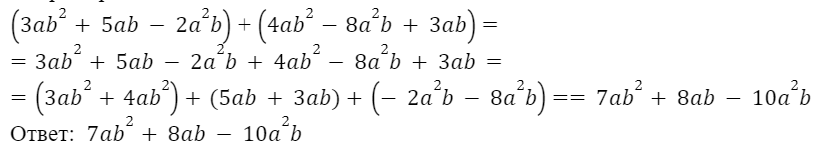
Вычитание многочленов

Например

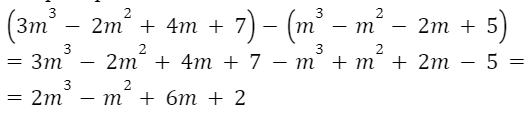
Ответ:

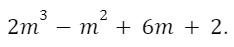
Умножение одночлена на многочлен

• Выполнив тождественное преобразование, используя распределительное свойство умножения, получим многочлен:

Умножение одночлена на многочлен

Для умножения одночлена на многочлен умножаем одночлен на каждый член многочлена и находим сумму результатов.

Например:

Вынесение общего множителя за скобки

• найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен
• найти переменные, которые встречаются в каждом члене. Переменные выносятся за скобки в наименьшей встречающейся степени, а также выполнить произведение коэффициента и общей буквенной части. 

Например:

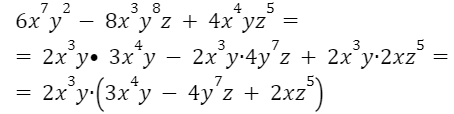
Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить

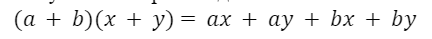
Например:

Выполните умножение:

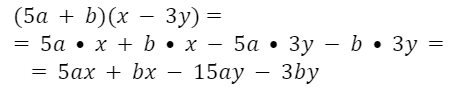
Задание

Даны следующие многочлены

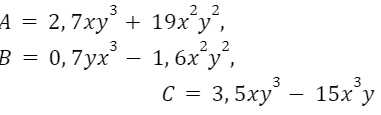
  Упростите выражение A-B+C 

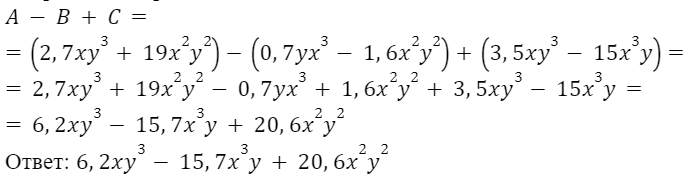
5.Найдите площадь закрашенной части фигуры. 

Решение: