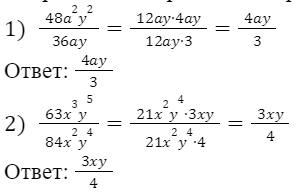Урок 11. Алгебраическая дробь и её основное свойство - Материалы к изучению
Здравствуйте, ученики!
Сегодня на уроке:
- узнаете алгебраические дроби и научитесь находить множество возможных значений переменных в алгебраической дроби;
- научитесь пользоваться основным свойством алгебраической дроби.
Алгебраическая дробь — это дробь, числитель и знаменатель которой являются многочленами.
Например:
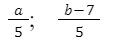
Область допустимых значений (ОДЗ)
Под областью допустимых значений (ОДЗ) понимают множество всех допустимых значений переменных для данного выражения.
Например:
Алгебраическая дробь и ее основные свойства
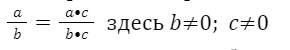
Тождественное преобразование выражения – это замена исходного выражения на выражение, тождественно равное ему.
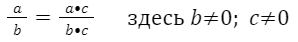
Используя тождественное преобразование, мы можем сократить дробь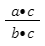 
до множителя c.
Если мы изменим знак числителя (или знаменателя) дроби, то изменится и знаменатель дроби.
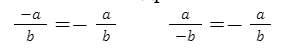
т. е. при изменении знака дроби меняется знак его числителя (или знаменателя).
Например:
Сократите дробь:
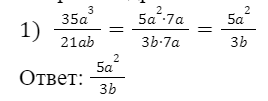
Пример 1:
При каких значениях переменной в составе алгебраической дроби
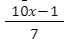
дробь равна нулю?
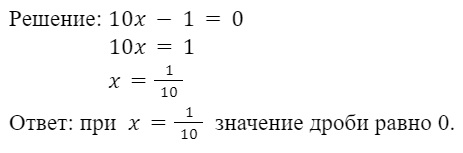
Пример 2:
Найдите область допустимых значений алгебраической дроби:
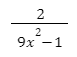
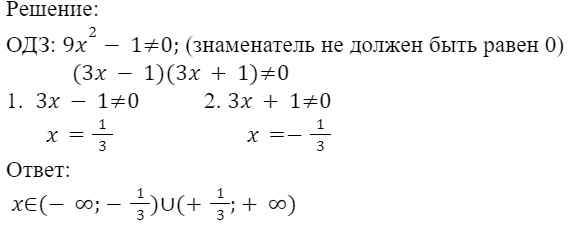
Пример 3:
При каких значениях дробь a равна нулю?
Пример 4. При каком значении переменной алгебраическая дробь не имеет смысла.
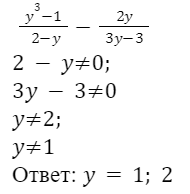
Пример 5:
При каких значениях дробь a равна нулю?
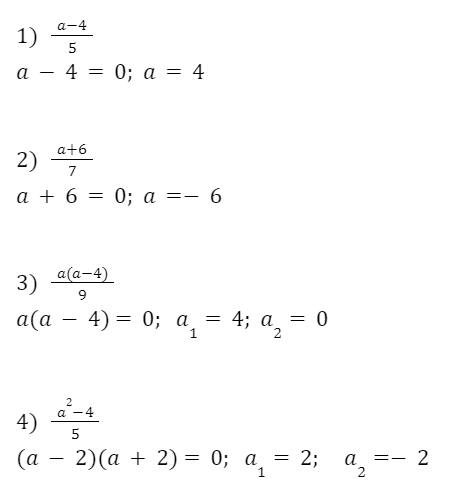
Пример 6.
Сократите дробь:
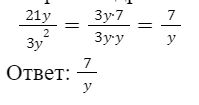
Пример 7.
Сократите дробь:
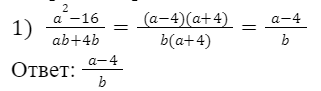
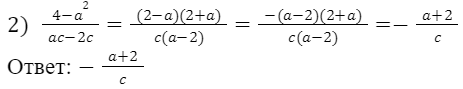
Пример 8.
Сократите алгебраические дроби:
