Сабақ 5. Функция - Оқу материалдары

Сәлеметсіздер ме, оқушылар! 

Бүгінгі сабақта: 

• функция және функцияның графигі ұғымдарын меңгересіздер; 
• функцияның берілу тәсілдерін білетін боласыздар
• y=kx функциясының анықтамасын біліп, графигін салып, k коэффициентіне  қатысты орналасуын анықтайсыздар;  
• y=kx+b түріндегі сызықтық функцияның анықтамасын біліп,  оның графигін салып және графиктің k және b коэффициенттеріне  қатысты орналасуын анықтайсыздар

«Функция» термині латынның functio деген сөзінен шыққан. Аудармасы: «орындау, атқару» деген мағынаны береді.  Бұл терминді тұңғыш рет 1694 жылы неміс математигі, ғалым Готфрид Вильгельм Лейбниц (1646-1716) енгізген.

Анықтама. Тәуелсіз айнымалының әрбір мүмкін мәніне тәуелді айнымалының жалғыз ғана мәні сәйкес болатын тәуелділікті функционалды тәуелділік немесе функция деп атайды.

Бұл анықтама нұсқасын ұсынған орыс математигі Николай Иванович Лобачевский (1792-1856). 

Тәуелсіз х айнымалыны аргумент деп атаймыз;

Тәуелді у айнымалысын – х аргументіне тәуелді функция деп атаймыз. 

 y = f(x)

1-мысал. Автомобиль тас жолда 80 км/сағ тұрақты жылдамдықпен жүріп келеді. Оның t уақытта жүріп өтетін S км жолын табу керек. 

Шешуі:

Бір айнымалы t тәуелсіз айнымалы өзгерсе, екінші айнымалы S тәуелді 

айнымалы өзгеріп отыратынын көрдік.
 

Тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының тек бір мәні сәйкес келетіні анықталды.

Функцияны анықтау үшін:

1) Функционалды тәуелділікті орнататын f заңдылығы берілуі керек. Ол формуламен (өрнекпен) де беріледі.  Бұл жағдайда функцияны аналитикалық жолмен берілді деп есептейді.  

Мысалы:  

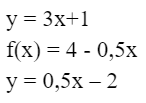
2) Аргументтің мүмкін мәндер жиыны көрсетілуі қажет. Бұл жиынды функцияның анықталу облысы деп атайды.

y = f(x) функиясының барлық қабылдайтын мәндері жиынын оның мәндер облысы деп атайды.

Мысалы:  

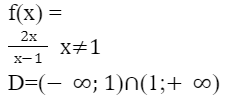
Функцияның берілу тәсілдері

Аналитикалық: мысалы у=2х+1

1. Кестемен беру

1. Графиктік тәсілі

1. Ауызша тәсіл: тәуелді айнымалы тәуелсіз айнымалының екі еселенген мәнінен 1-ге артық.

Тура пропорционалдық функциясы

Формуласы:  y=k∙x мұнда   k- берілген тұрақты сан, оны пропорционалдық коэффициент деп атайды. Анықталу облысы: -∞;+∞.

Тура пропорционалдық функцияның қасиеттері 

1. х және у айнымалыларының әртүрлі сәйкес мәндері өзара пропорционал, яғни 

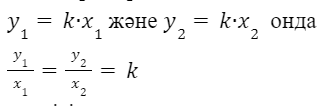
теңдігі орындалады.

Сондықтан k-пропорционалдық коэффициент деп аталады. 

Оны сәйкес түзудің бұрыштық коэффициенті деп те атайды. Өйткені k саны у=kx графигі мен Ох осі арасындағы бұрышқа тәуелді болады.

1. у=kx функциясының графигі - координаталар жүйесінің бас нүктесі О(0;0) арқылы өтетін түзу сызық.  

1-мысал.

у=2х функциясының графигін салыңыз.  

Шешуі: кесте құрастырамыз. у=2х   

y=2∙-4=-8 

y=2∙-3=-6

y=2∙-2=-4

y=2∙-1=-2

y=2∙0=0

y=2∙1=2

y=2∙2=4

y=2∙3=6

y=2∙4=8

нәтижесінде алынған нүктелерді  координаталық жазықтықта бейнелейміз немесе қысқаша у=2х функциясының графигін салайық.  

Шешуі: кесте құрастырамыз. у=2х.

Түзу салу үшін екі нүкте жеткілікті.

нәтижесінде алынған нүктелерді  координаталық жазықтықта бейнелейміз.

Сызықтық функция және оның графигі у=kx+b сызықтық функция деп аталады 

k және  b – берілген сандар. 

k – бұрыштық коэффициент деп, 

ал b бос мүше деп аталады.

х=0 болса,   онда у=b болады. 

графигі Оу осін (0; b) нүктесінде қиып өтетін түзу. Сызықтық функция және оның графигі у=kx+b

1 -мысал.

y=0,5∙x-1  функциясының графигін салу керек.

Шешуі: мәндер кестесін құрамыз.