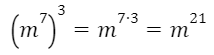Сабақ 1. Натурал көрсеткішті дәреже және оның қасиеті - Оқу материалдары
Сәлеметсіздер ме, оқушылар! Бүгінгі сабақтың тақырыбы Натурал көрсеткішті дәреже және оның қасиеті.
Алгебра – математиканың бір бөлігі. Орта Азия математигі және астрономы Мұхаммед әл-Хорезми «Китаб аль-джебр валь-мукабала» атты еңбегінде бір дәрежелі теңдеулерді шешудің жалпы ережелерін келтірген.«Аль-джебр» (қайта қалпына келтіру деген мағынада). «Аль-джебр» сөзінен «алгебра» атауы туындаған.
Егер а – кез келген сан, ал n – бірден үлкен немесе бірге тең натурал сан болса, онда а санының өз-өзіне n рет көбейтіндісі а санының n-ші дәрежесі деп аталады.
а (n дәріжесі) мұнда n>1.
мұндағы а саны – негізі деп, n натурал саны – дәреже көрсеткіші деп аталады
(-2)3 = (-2)∙-2-2 = -8.
Қасиеттері:
1. ДӘРЕЖЕЛЕРДІ КӨБЕЙТУ
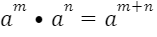
Мысалы:
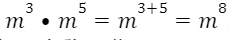
Негіздері бірдей дәрежелерді көбейткенде олардың дәреже көрсеткіштерін қосып, негізін өзгеріссіз қалдырамыз.
2. ДӘРЕЖЕЛЕРДІ БӨЛУ
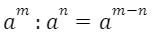
Мысалы:
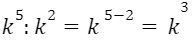
Негіздері бірдей дәрежелерді бөлгенде бөлінгіштің дәреже көрсеткішінен бөлгіштің дәреже көрсеткішін азайтып, негізін өзгеріссіз қалдырамыз.
3. Нөлден өзге а санының 0 дәрежесі 1-ге тең.
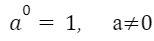
Мысалы:
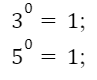
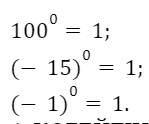
4. КӨБЕЙТІНДІНІ ДӘРЕЖЕГЕ ШЫҒАРУ
Кез келген а және b сандары мен кез келген натурал n саны үшін:
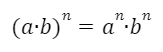
Мысалы:
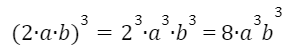
Көбейтіндіні дәрежеге шығару үшін көбейткіштердің әрқайсысын осы дәрежеге шығарып, нәтижелерін көбейтеміз.
5. Теріс санның жұп дәрежесі – оң сан, ал, тақ дәрежесі –теріс сан болады.
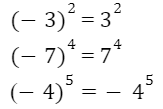
6. БӨЛШЕКТІ ДӘРЕЖЕГЕ ШЫҒАРУ
Бөлшекті дәрежеге шығарғанда, оның алымын да, бөлімін де жеке-жеке сол дәрежеге шығарамыз.
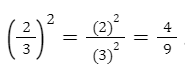
7. ДӘРЕЖЕНІ ДӘРЕЖЕГЕ ШЫҒАРУ
Кез келген а саны мен кез келген m және n сандары үшін
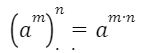
теңдігі орындалады.
Дәрежені дәрежеге шығарғанда, негізін өзгертпей дәреже көрсеткіштерін өзара көбейтеміз.
Мысалы: